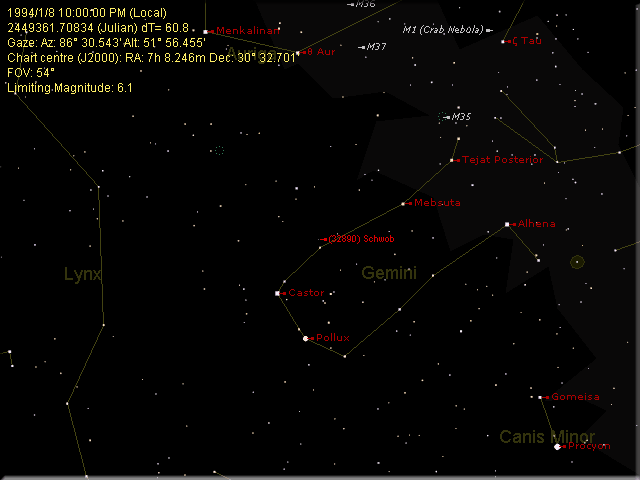
Minor Planet (32890) Schwob = 1994 AL1

Mars-crossing Asteroid
Discovered 1994 January 8 by
Carolyn S. Shoemaker and David H. Levy at Palomar.

As the result of an extraordinarily gracious request by their discoverers,
asteroid 32890 is named "Schwob" by the IAU's MPC on 28 September 2004.

1994 AL1
Position of (32890) Schwob in Gemini the night of its discovery [Top-of-page]


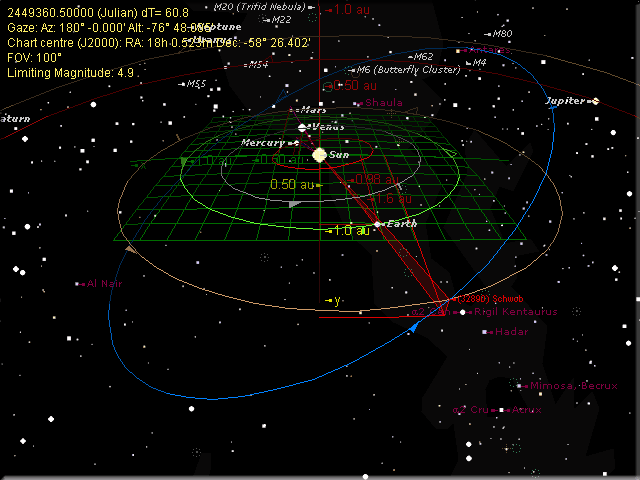
Click for the current NASA orbit diagram
Orbits of the inner planets and position of (32890) Schwob at discovery
Click the picture for the current NASA orbit diagram - java must be enabled (goes off-site) [Top-of-page]

You can download a Quicktime animation of (32890) Schwob making a complete orbit around the Sun
from 2004 March 5 to 2006 October 5. Each frame represents 2 days. (Warning: It's a fairly large file at 5.2Meg.)


Facsimile of the IAU's Minor Planet Center
Circular No. 52770, dated 2004 Sept. 28
(32890) Schwob = 1994 AL1

Discovered 1994 January 8 by
C. S. Shoemaker and D. H. Levy at Palomar

Named in honor of Pierre Schwob (b.1946), a software engineer whose eclectic interests bring together studies in cosmology and in comets. Dividing his interest between the Kavli Institute for Particle Astrophysics and Cosmology, and the Jarnac Comet Survey, Schwob also manages to find time for his writings on classical music, pocket calculators, and chess.

Thank you David, Wendee, and Carolyn!
My family and I will be eternally grateful.
[Top-of-page]

David Levy and PRS
David Levy and Pierre during a visit at the Levy's home in Vail, Arizona. May 2003
[Top-of-page]

Orbital data
Source: neo.jpl.nasa.gov - See the definitions below

Epoch (MJD) 2456399.5 (2013-Apr-17.00 )
a = Semi-major Axis Distance (A) 1.882559945333079 AU
e = Eccentricity (EC) .16677303571014
i = Inclination (IN) 28.56608664498119 deg
Ω = Longitude of the Ascending Node (OM) 101.1854650502225 deg
q = Perihelion Distance (QR) 1.568599708343566 AU
w = Argument of Perihelion (W) 54.0452390366029 deg
Q = Aphelion Distance (ADIST) 2.196520182322591 AU
M = Mean Anomaly (L) 151.6330626 deg
P = Orbital Period (PER) 2.58304 y
n = Mean Motion (N) .381575815 deg/d
RotPer = Rotation Period 7.93 hours
H = Absolute Magnitude (H) 15.5
G = Magnitude Slope parameter (G) 0.150
Est. diameter (with typical albedo of 0.05 to 0.25) 2.016 to 4.508 km (1.253 to 2.801 miles)
[Top-of-page]


PRS at Lick
Pierre at the Lick Observatory where he hopes to image (32890) Schwob [Photo Rem Stone] [Top-of-page]




Return to my own site or visit Pierre's astronomy trips page

A Few Definitions

Astronomical Unit (AU)
An Astronomical Unit is the mean distance between the Earth and the Sun. It is a derived constant and used to indicate distances within a solar system. The Earth orbits at a distance of 1 AU from the Sun.

Argument of Perihelion
The angle (in the body's orbit plane) between the ascending node line and perihelion measured in the direction of the body's orbit.

Eccentricity
An orbital parameter describing the eccentricity of the orbit ellipse. Eccentricity e is the ratio of half the distance between the foci c to the semi-major axis a: e=c/a. For example, an orbit with e=0 is circular, e=1 is parabolic, and e between 0 and 1 is elliptic.

Inclination
The angle between the vectors normal to the body's orbit plane and the specified reference plane. Typical reference planes are the ecliptic plane and the equatorial plane (referred to a specific epoch).

Longitude of Perihelion
The sum of the longitude of the ascending node and the argument of perihelion.

Longitude of the Ascending Node
The angle between the reference X-direction (typically the vernal equinox) and the point at which the body passes up (north) through the reference plane.

Mean Anomaly
The product of an orbiting body's mean motion and time past perihelion passage.

Mean Longitude
The sum of the mean anomaly and the longitude of perihelion.

Mean Motion
The angular speed required for a body to make one orbit around an ideal ellipse with a specific semi-major axis.

Orbital Period
The time required for an object to make a complete revolution along its orbit. For example, the orbital period for a typical main-belt asteroid is about 4 years.

Perihelion Distance
The distance between the orbiting body and the sun at its closest approach.

Semi-major Axis
Half the length of the major axis of an orbit ellipse.

Time of Perihelion Passage
The time at which an object is at perihelion (its closest distance to the sun).

[Top-of-page] Return to my site or visit Pierre's astronomy trips page